Logistic Regression
6 min read

Can you predict success in exams?
Have you ever helped your younger sibling prepare for a big exam,
and thought to yourself why do some students seem to breeze through exams effortlessly,
while others struggle despite putting in long hours? And that can there be a way to predict
whether a student will pass or fail based on their study hours?
Let’s delve into this
problem. Understanding how different factors influence exam outcomes leads us to introduce a
vital statistical tool - Logistic Regression!
Understanding Logistic Regression
Logistic regression is a method effective for predicting categorical outcomes. Yes, categorical outcomes like categorizing if a student passes or fails an exam based on their study hours.
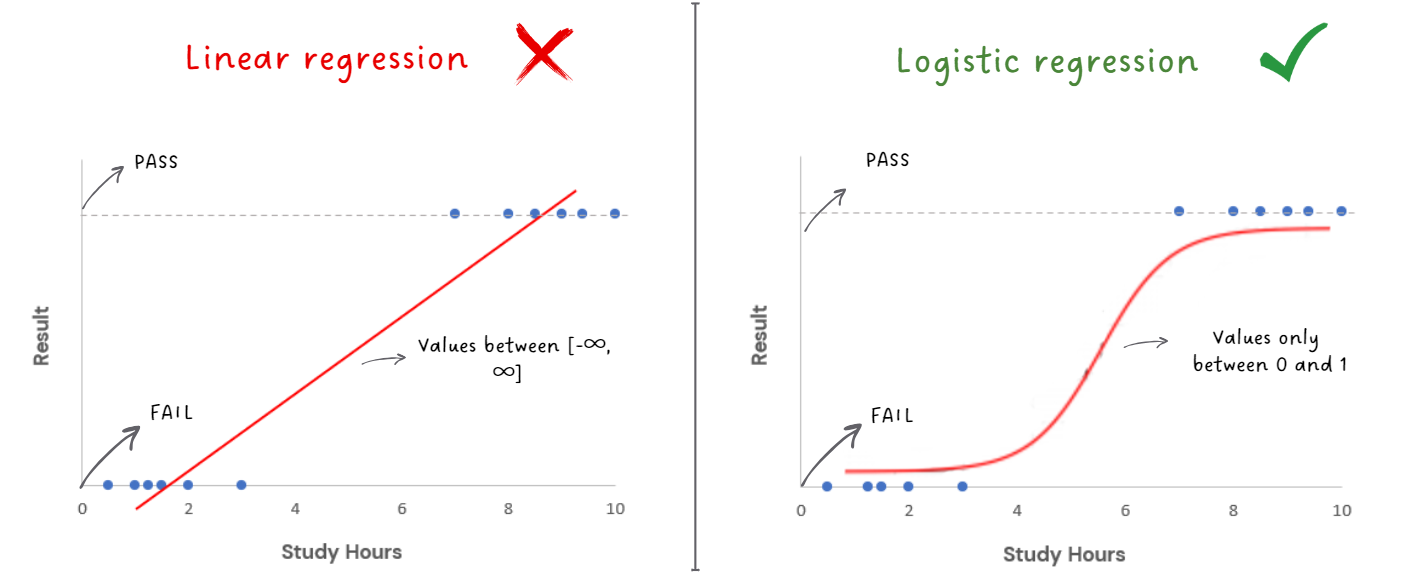
But why not use Linear Regression in this case?
Because linear regression outputs values across the entire range of [-∞, ∞], but in our case, we're dealing with 'pass' or 'fail,' like flipping a light switch on or off. Hence, we require a function yielding - 'pass' or 'fail', 'yes' or 'no', 0 or 1 - for any given input.
How does logistic regression work?
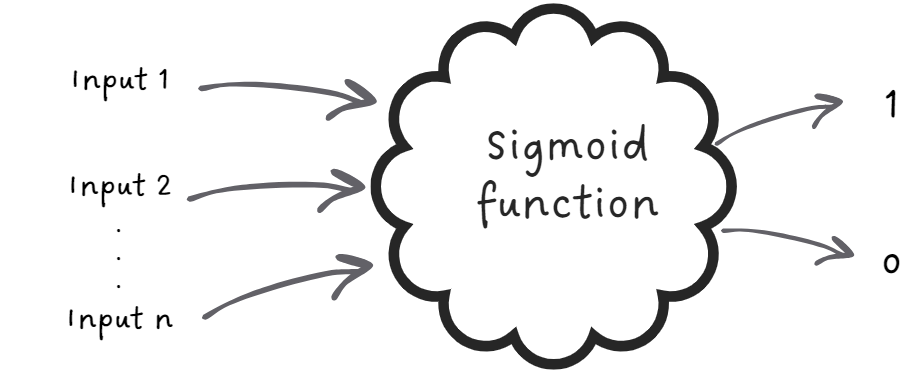
Let’s start by understanding the sigmoid function.
The sigmoid function, also known as the logistic function, is an S-shaped curve smoothly
transitioning between 0 and 1 as the input changes. In the pass-fail example, the
sigmoid curve takes the study hours as input and maps them to the probability of passing
the exam. The curve starts low, then gradually rises, and eventually levels off at
nearly 1.
Imagine a black box that takes different study hours as inputs, and
outputs probabilities of passing or failing the exam that is then mapped to either a 0
(fail) or a 1 (pass)
With the continuous probability between 0 and 1, how is it determined whether the student passes or fails?
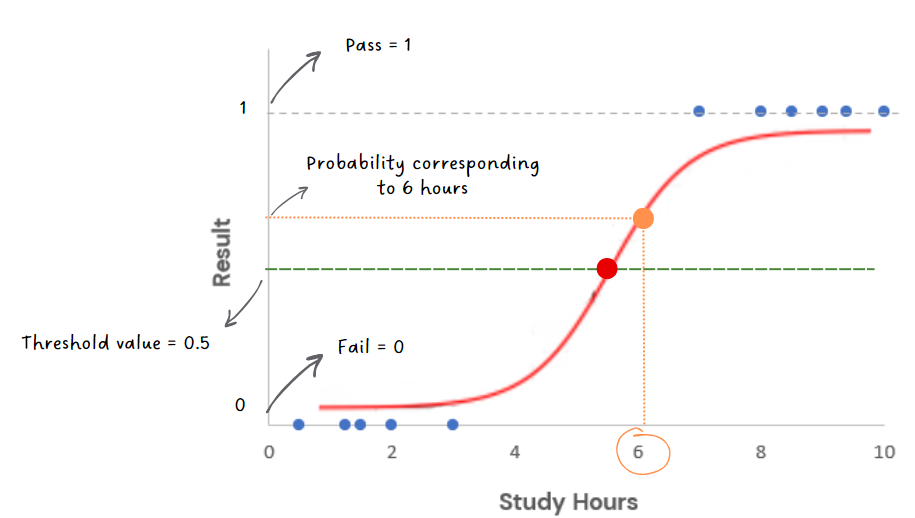
Choosing the right threshold
The point on the sigmoid curve represents the probability of
passing or failing the exam. Now imagine the point on the sigmoid curve where it
transitions from predicting 'fail' to predicting 'pass.' This is the threshold value. In
the context of our pass-fail example, this value represents the study hours at which we
would say, 'Okay, if the probability of passing is above this point, we predict 'pass,'
and if it's below, we predict 'fail.''
In the graph below, we have assumed the threshold to be 0.5. If the student studies for
6 hours, the probability of passing the exam becomes >0.5, and hence the student would
be predicted as 'Pass'
Choosing the threshold involves finding a balance. Opting for a
higher threshold means we predict fewer 'pass' cases but with higher accuracy.
Conversely, opting for a lower threshold includes more 'pass' predictions, yet it may
lead to false positives – instances where we predict a 'pass' but the student actually
didn't.
Do you now wonder, just like we do, how are the study hours converted to probability?
Converting study hours to probability
To understand this let's bring everything we learned so far
together and expand upon that.
Imagine we have a dataset filled with information about how many hours students studied
and whether they passed or failed. This is known as our training data. The objective of
logistic regression is to build a formula that, when given the number of hours a student
studied, can tell whether they passed or failed.
When we input the hours studied into this formula, it gives us a probability score,
which when close to 0, indicates that we are confident that the student has failed, and
when close to 1 indicates that the student has passed. But how do we know if our formula
is good?
That's where the concept of error comes in.
Error is the difference between how sure our formula is and what actually happened. If
our formula says a student passed with a high probability, but they actually failed, the
error is high. On the other hand, if our formula hesitated and said they might fail, and
they did fail, the error would be lower.
When we add all these errors for all the students in our training data, we get the total
error. If you are now thinking if we need to minimize the errors, then you are on the
right path.
How do we minimize the errors though?
We use the same old optimization techniques like gradient descent, a method that helps us iteratively test different parameter values until we find the ones that yield the lowest overall error.
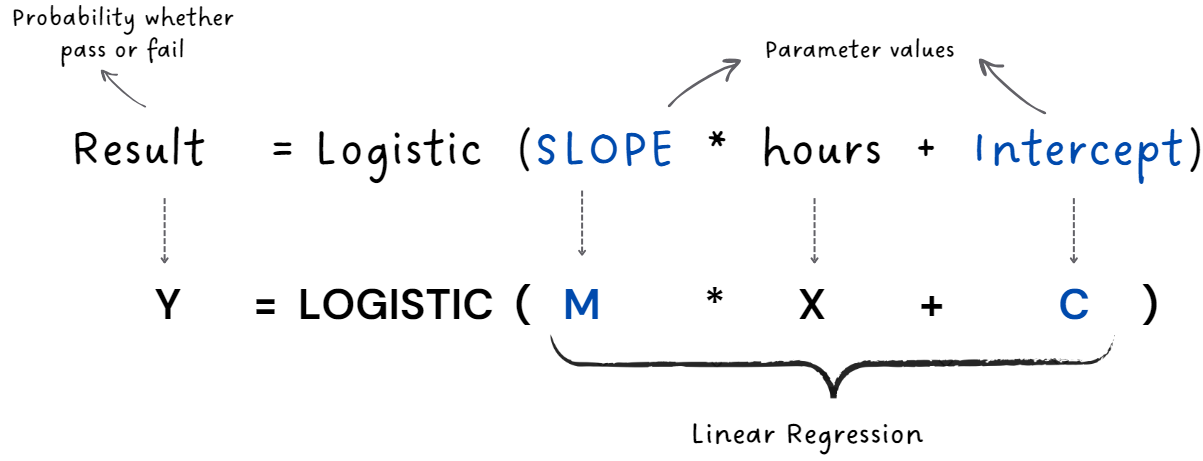
The equation for the line remains unchanged from linear regression, but a Logistic function is introduced at the beginning. This Logistic function serves to compress the values, ensuring they are within the range of 0 to 1.
What if we have more than 2 categories?
Let's say we want to predict whether a student will score below
50, between 50 to 80, or above 80 marks. You might ask if logistic regression can handle
such cases.
It can.
While our detailed discussion focused on binary classification with just two classes, we
can expand it to multiple classes, which is known as multiclass classification. So,
whether you're classifying different flower species, or diagnosing illnesses, logistic
regression can be a dependable tool for all such tasks.
Real-World Business Use-Case
Empowering Healthcare with Data-Driven Patient Insights
Imagine a medical research institute striving to improve patient
outcomes by identifying the likelihood of a certain medical condition based on various
patient characteristics. The institute has gathered vast datasets containing patient
profiles, medical histories, genetic markers, and diagnostic test results.
In this context, logistic regression serves as a powerful classification tool. By
examining the relationships between patient attributes such as age, family history,
genetic markers, and test results, logistic regression can predict the probability of a
patient having a specific medical condition.
For instance, it might unveil that patients with a certain genetic marker and a family
history of the condition are more likely to develop the medical condition. Conversely,
patients with certain test results falling within a certain range might exhibit a lower
probability of having the condition.
Armed with these insights, the medical research institute can enhance its diagnostic
processes, develop personalized treatment plans, and allocate resources more
efficiently. In a field where early detection and targeted interventions are crucial,
leveraging logistic regression's predictive capabilities can lead to improved patient
care, and advancements in medical research.
Have any burning questions or specific topics you'd like us to explore? Share your thoughts at hi@simplifyingstuff.com
